Sind totale Sonnenfinsternisse im Sommer häufiger?
1.) die Mondschatten bei Sonnenfinsternissen
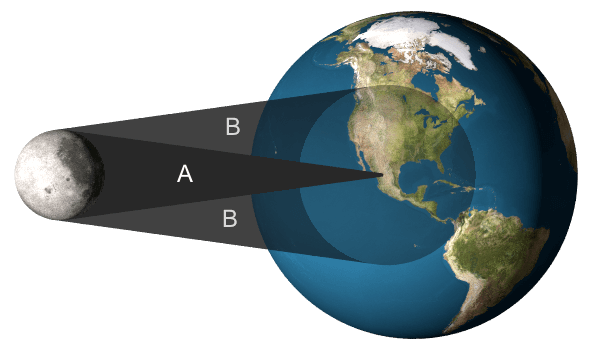
Bild 1
Bild 1 zeigt die Schatten der totalen Sonnenfinsternis vom 8. April 2024 in Mexiko.
Der Schattenkegel A wird Umbra oder Kernschatten genannt und trifft die Erdoberfläche in einem kleinen Kreis.
Dort kann überall Totalität beobachtet werden.
Ein weitaus größerer Ring von Schatten B mit der Bezeichnung Penumbra oder Halbschatten zeigt den Bereich auf der Erdoberfläche an,
bei dem noch eine Teilverfinsterung der Sonne zu sehen ist.
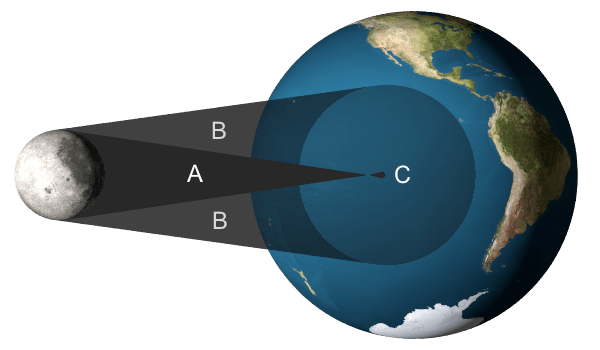
Bild 2
Bild 2 zeigt die ringförmige Sonnenfinsternis am 2. Oktober 2024 über der Osterinsel.
Dabei gibt es einen weiteren Schattenbereich C mit der Bezeichnung Antumbra oder Ringschatten,
der auch bei der totalen Sonnenfinsternis existiert, aber in die Erde eingetaucht und daher nicht sichtbar ist.
2.) die Bedingungen für totale Sonnenfinsternisse
Es gibt 3 Bedingungen für eine von der Erdoberfläche beobachtbare totale Sonnenfinsternis:
- Sonne und Mond müssen auf der gleichen ekliptikalen Länge sich treffen, das ist bei Neumond der Fall.
Für die Berechnung der Länge der Sonne und des Mondes gibt es im Anhang komplizierte Formeln.
Während die Sonne in 365,25636 Tagen (${T_S}_{sid}$) einen vollen Umlauf auf der Ekliptik vollführt ist der Mond sehr viel schneller.
Er benötigt auf seiner Bahn im Mittel nur 27,321662 Tage für einen Umlauf von 360°. Das ist die siderische Periode (${T_M}_{sid}$).
Tatsächlich muss er von einem Neumond zum nächsten noch etwas weiter laufen,
weil die Sonne in dieser Zeit auch einen Winkel von etwa 29° vorangeschritten ist.
Die Zeit von Neumond zu Neumond beträgt deshalb gegenwärtig im Durchschnitt 29,53058867 Tage, die synodische Periode (${T_M}_{syn}$).
$$\text{Zusammenhang der Zeiten: } \frac1{{T_M}_{syn}}+\frac1{{T_S}_{sid}}=\frac1{{T_M}_{sid}}$$
Daraus folgt, dass ein Zusammentreffen etwa 12,4 mal pro Jahr jeweils bei Neumond sich ereignet.
Die Mitte einer Sonnenfinsternis findet immer zeitlich dicht bei Neumond statt.
Die Zeitdifferenz von Finsternis zu Neumond liegt im Minutenbereich.
- Die Sonne läuft genau auf der Ekliptik, also in ekliptikaler Breite immer bei 0°. So ist die Ekliptik auch definiert.
Der Mond hat eine Umlaufbahn, die etwas mehr als 5° gegen die Ekliptik-Ebene geneigt ist.
Bild 3
Das Bild 3 zeigt die Mondbahn mit übertriebenem Neigungswinkel, Inklination genannt.
Daher ist die ekliptikale Breite des Mondes innerhalb eines Monats schwankend zwischen +5° und -5°.
Dabei gibt es zwei Punkte auf der Bahn, bei der die Breite 0° ist, das sind die Knotenpunkte,
die abwechselnd den Nullpunkt aufsteigend und absteigend durchqueren.
Die Bedingung für Sonnenfinsternisse sind nur in einem engen Bereich in der Nähe der Knoten erfüllt, etwa - 1,4° bis + 1,4° ekliptikaler Breite.
Für die Berechnung dieses Wertes gibt es im Anhang ebenfalls eine komplizierte Formel.
Oftmals wird die Bedingung auch mit dem Winkelabstand zum Knoten angegeben oder noch besser als Gammawert ($\gamma$).
bei Umrechnungen ist aber immer der Ausgangswert die ekliptikale Breite.
Der Wert von Gamma berechnet sich aus der ekliptikalen Breite des Mondes zur Zeit der Finsternis und seiner Entfernung, normiert auf den Erdradius:
$\gamma=\text{Gamma} = \frac{\sin(Mondbreite)\,\cdot\,Mondentfernung}{Erdradius}$
Der Wert der Magnitude kann aus dem Verhältnis von $\frac{Mondradius}{Mondentfernung}$ zu $\frac{Sonnenradius}{Sonnenentfernung}$ berechnet werden,
denn die beiden Quotienten sind die scheinbaren Radien aus Sicht der Erde:
$\text{Magnitude} = \frac{Mondradius\,\cdot\,Sonnenentfernung}{Mondentfernung\,\cdot\,Sonnenradius}$
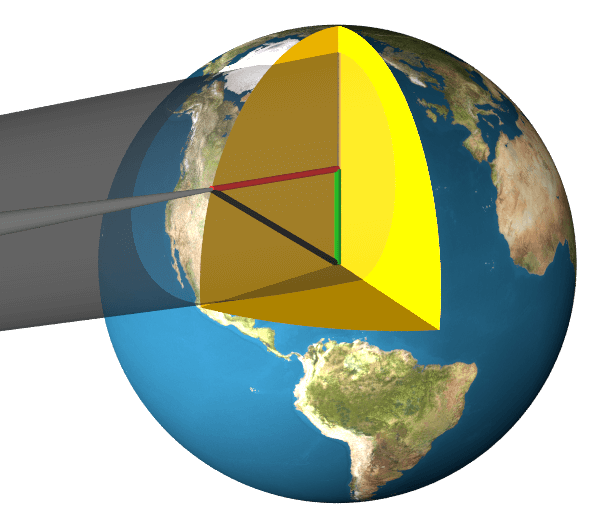
Im folgenden Bild 4 ist ein Dreieck eingezeichnet. Die Längen der Seiten sind:
$$\begin{align}
\text{grüne Seite}&=\gamma\cdot Erdradius \\
\text{schwarze Seite}&=Erdradius \\
\text{rote Seite}&={\textstyle\sqrt{1-\gamma^2}}\cdot Erdradius
\end{align}$$
Bild 4
Die Länge der roten Seite muss bei der Berechnung der Mondentfernung für die Magnitude berücksichtigt werden.
Die im Anhang angegebene Formel für die Mondentfernung ist der Abstand von Mondmittelpunkt bis Erdmittelpunkt.
Von diesem Wert muss die Länge der roten Seite abgezogen werden.
- Es gibt verschiedene Arten von Sonnenfinsternissen:
- totale finden statt, wenn die Mondscheibe größer als die Sonnenscheibe am Himmel erscheint (Magnitude größer 1).
- ringförmige finden statt, wenn die Mondscheibe kleiner als die Sonnenscheibe am Himmel erscheint (Magnitude kleiner 1).
- hybride finden statt, wenn in der Mitte der Finsternis die Mondscheibe größer als die Sonnenscheibe am Himmel erscheint,
aber anfangs und zum Ende des Finsternisstreifens auf der Erde die Mondscheibe kleiner ist.
Dies ist eine Folge des größeren Abstands (plus Anteil vom Erdradius) der Erdoberfläche vom Mond.
- partielle finden statt, wenn der Kernschatten oder Ringschatten nicht auf die Erdoberfläche trifft
sondern hoch über dem Nordpol oder tief unter dem Südpol entlang läuft, aber der Halbschatten noch die Erde erreicht.
3.) Berechnung der Größe der Mondschatten
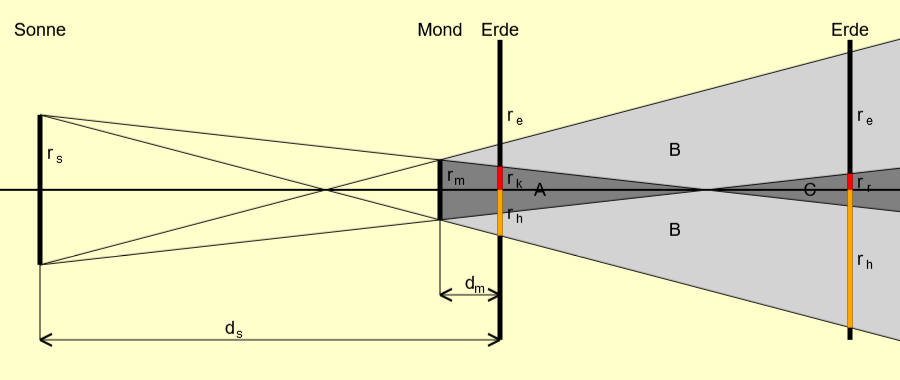
Bild 5
Im Bild 5 ist schematisch der Schattenwurf des Mondes auf die Erde gezeigt.
Die Erde ist gleich zweimal an unterschiedlichen Positionen vorhanden:
in Bildmitte bei einer totalen Sonnenfinsternis und rechts bei einer ringförmigen Sonnenfinsternis.
Alle Abmessungen sind nicht maßstäblich sondern so gewählt, dass die Radien der Schatten deutlich erkennbar sind.
Die Bezeichnungen sind:
$$
r_s=\text{Radius der Sonne}\\
r_m=\text{Radius des Mondes}\\
r_e=\text{Radius der Erde}\\
r_k=\text{Radius des Kernschattens (rot)}\\
r_r=\text{Radius des Ringschattens (rot)}\\
r_h=\text{Radius des Halbschattens (orange)}\\
d_s=\text{Distanz zwischen Erdoberfläche und Sonnenmittelpunkt}\\
d_m=\text{Distanz zwischen Erdoberfläche und Mondmittelpunkt}
$$
Mit einfachen geometrischen Mitteln, z.B. Ähnlichkeit von Dreiecken oder Strahlensatz, kann man zu folgenden Berechnungen kommen:
$$
\rand{r_k=\frac{r_m\cdot d_s-r_s\cdot d_m}{d_s-d_m}≈r_m-r_s\cdot\frac{d_m}{d_s}}
$$
und
$$
\rand{r_h=\frac{r_m\cdot d_s+r_s\cdot d_m}{d_s-d_m}≈r_m+r_s\cdot\frac{d_m}{d_s}}
$$
Wird $r_k$ negativ so nimmt man stattdessen
$$
\rand{r_r=-r_k}
$$
Für die totale Sonnenfinsternis in Bild 1 berechnen sich die Schattenradien wie folgt:
$$
JD=2460409,2621=\text{Mo 8. Apr. 2024⠀18:17}\\
Magnitude=1,0568\\
Gamma=0,3426\\
r_s=696342\text{ km}\\
r_m=1737,4\text{ km}\\
d_s=149823049\text{ km}\\
d_m=353735\text{ km}\\
\rand{r_k=93,324\text{ km}}\\
\rand{r_h=3381,476\text{ km}}
$$
Für die ringförmige Sonnenfinsternis in Bild 2 berechnen sich die Schattenradien wie folgt:
$$
JD=2460586,2838=\text{Mi 2. Okt. 2024⠀18:48}\\
Magnitude=0,9327\\
Gamma=-0,3517\\
r_s=696342\text{ km}\\
r_m=1737,4\text{ km}\\
d_s=149705775\text{ km}\\
d_m=400473\text{ km}\\
r_k=-125,360\text{ km}\\
\text{also }\rand{r_r=125,360\text{ km}}\\
\rand{r_h=3627,901\text{ km}}
$$
Die Werte für $r_k$ und $r_r$ sind ein Maß für die Dauer der Totalität bzw. Ringform.
Für die Breite des Finsternisstreifens muss eine Korrektur für die Verformung des Schattens auf der gekrümmten Erdoberfläche vorgenommen werden.
Der Kreis wird dann näherungsweise zur Ellipse mit einer großen Halbachse in Nord-Süd-Richtung.
Dazu multipliziert man $r_k$ und $r_r$ mit dem Faktor $\sqrt{\frac1{1-\gamma^2}}$.
Die Radien von Sonne, Mond und Erde können auch im Weiteren als konstant angenommen werden,
hingegen ändern sich die Abstände von Sonne und Mond zur Erde dauernd.
Dafür gibt es auch komplizierte Berechnungsformeln, die im Anhang gelistet sind.
4.) die Jahreszeiten und ihre Veränderlichkeit
Da nach den totalen Sonnenfinsternissen im Sommer gefragt wurde, muss zunächst geklärt werden welcher Zeitraum des Jahres gemeint ist.
Sinnvoll ist das Sommerhalbjahr von der Frühlings-Tagundnachtgleiche bis zur Herbst-Tagundnachtgleiche,
also etwa der Zeitraum, der bei uns mit Sommerzeit belegt wird.
Für das Jahr 2024 ergeben sich in Tabelle 1 folgende Daten:
| Ereignisse des Jahres 2024 | Datum und Zeit | Julianisches
Datum |
|---|
| Jahresbeginn | Mo 1. Jan. 2024⠀00:00 | 2460310,5000 |
| Frühlingsanfang (Tagundnachtgleiche) | Mi 20. Mrz. 2024⠀02:57 | 2460389,6231 |
| Sommeranfang (Sommersonnenwende) | Do 20. Jun. 2024⠀20:41 | 2460482,3625 |
| Herbstanfang (Tagundnachtgleiche) | So 22. Sep. 2024⠀12:35 | 2460576,0248 |
| Winteranfang (Wintersonnenwende) | Sa 21. Dez. 2024⠀09:14 | 2460665,8848 |
| Perihel (Erde in Sonnennähe) | Mi 3. Jan. 2024⠀00:55 | 2460312,5386 |
| Aphel (Erde in Sonnenferne) | Fr 5. Jul. 2024⠀04:58 | 2460496,7071 |
Tabelle 1
Das Julianische Datum ist die Tageszählung seit dem Mo 24. Nov. -4713⠀12:00.
Astronomisch hat dieses Startdatum keine Bedeutung aber festgelegt wurde es im Jahre 1583 von Joseph Scaliger mit der Zielsetzung, den Zeitpunkt der Schöpfung festzulegen.
Heutzutage wird das Julianische Datum häufig in der astronomischen Berechnung verwendet, weil es Zeitpunkte und Zeiträume unabhängig von jeglichen Kalendern ermöglicht.
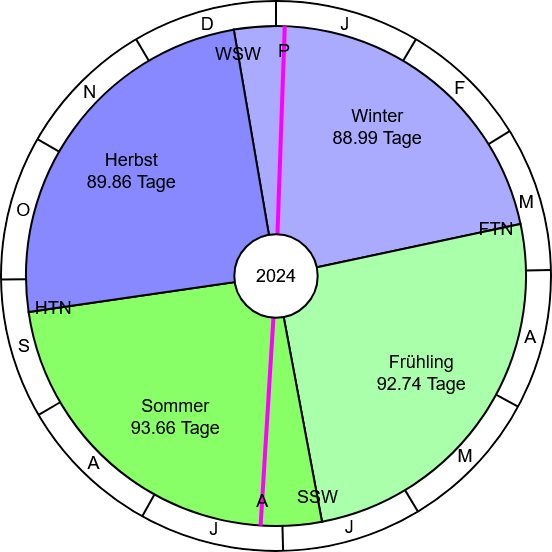
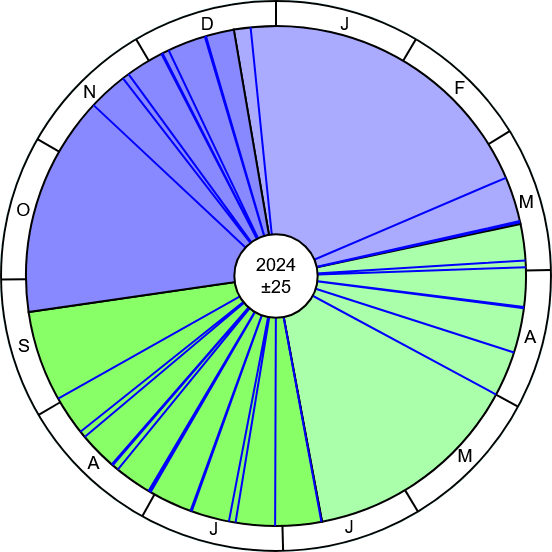
Die Daten der Tabelle 1 lassen sich auch mit folgender Jahreskreisdarstellung veranschaulichen:
Bild 6
Der Kreis zeigt im äußeren Ring die Monatsnamen mit dem ersten Buchstaben, beginnend ganz oben und weiter rechtsdrehend.
Die Farben sind: Winterhalbjahr blau und Sommerhalbjahr grün.
Die Dauer der Jahreszeiten sind deutlich unterschiedlich lang, eine Folge der Bahnellipse der Erdbahn.
Dort wo die Sonne am weitesten von der Erde entfernt ist (A = Aphel = Sonnenferne) sind die Jahreszeiten länger.
2024
Frühling + Sommer = 186,40 Tage
ist zurzeit 7,55 Tage länger als
Herbst + Winter = 178,85 Tage
Sommerhalbjahr / Winterhalbjahr = 1,042
Sommer + Herbst = 183,52 Tage
ist nur 1,80 Tage länger als
Winter + Frühling = 181,73 Tage
Jahreslänge = 365,25 Tage
Hauptursache für eine langfristige Veränderung der Länge der Jahreszeiten ist die Verschiebung des Frühlingspunktes gegenüber der großen Halbachse der Erdbahn-Ellipse.
Dabei ist die Präzession überwiegend beteiligt.
Dieser Effekt ist auch dafür verantwortlich, dass die Sonne inzwischen nicht mehr in dem Sternbild steht, welches z.B. nach den Horoskopen eigentlich „zuständig“ wäre.
Die Veränderung in der Lage der großen Halbachse ist geringer.
Sie tritt in dem Unterschied von siderischem zu anomalistischem Jahr zutage und wirkt sich in umgekehrter Richtung aus.
| tropisches Jahr | Tt | 365,24219878 Tage |
| siderisches Jahr | Ts | 365,25636556 Tage |
| anomalistisches Jahr | Ta | 365,25964134 Tage |
Aus den Zahlen der Tabelle folgt:
- die Sonne im Frühlingspunkt durchläuft in $T_t/(T_s-T_t)=25783 \text{ Jahre}$ alle Sternbilder des Tierkreises (Platonisches Jahr)
- ein Umlauf der großen Achse der Erdbahn-Ellipse dauert $T_t/(T_a-T_s)=111498 \text{ Jahre}$ in Gegenrichtung zur Frühlingspunktbewegung
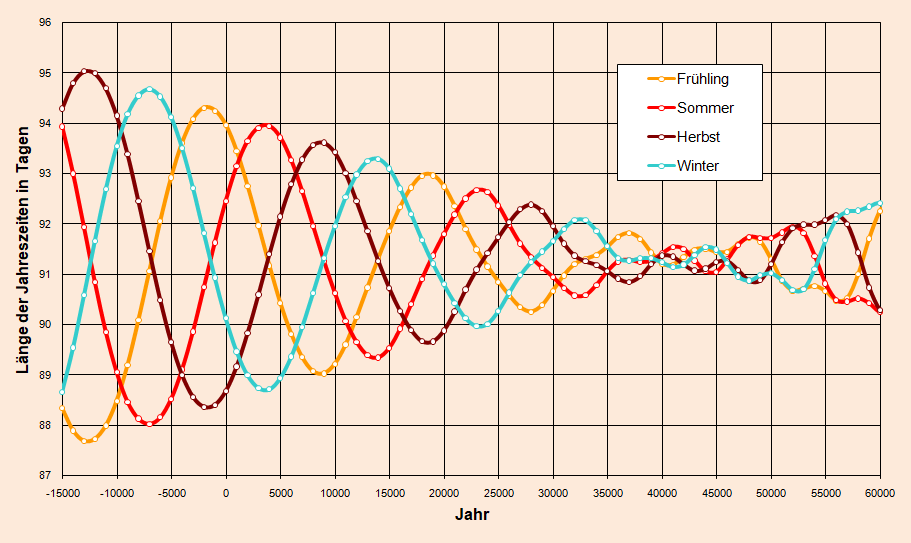
- die Jahreszeiten durchlaufen alle Abschnitte der Ellipse in $T_t/(T_a-T_t)=20940 \text{ Jahre}$ und genau das wird aus der folgenden Grafik ersichtlich.
Bild 7
Die Veränderung der Amplituden ist eine Folge der Änderung der Elliptizität der Erdbahn mit einer Periode von 400000 Jahren,
von der hier im Bild 7 nur $\frac16$ der Periode zu sehen ist.
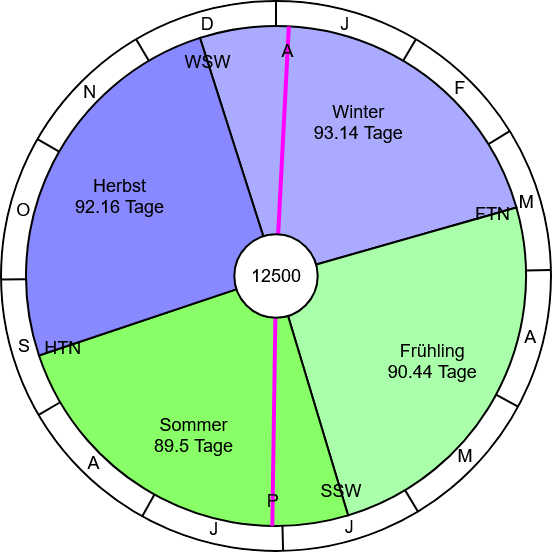
Wenn man nun 10500 Jahre in die Zukunft schaut erhält man folgendes Bild:
Bild 8
Hier sind die Sonnennähe (Perihel) und Sonnenferne (Aphel) im Jahreslauf vertauscht und natürlich wirkt sich das auch auf die Länge der Jahreszeiten aus.
Es sind dann Herbst und Winter die längsten Jahreszeiten.
Eine so lange Zeit hat auch auf unseren Kalender Auswirkungen: der Frühlingspunkt wandert Richtung Mitte März.
Es war schon bei der Kalenderreform von 1582 klar, dass spätere Anpassungen nötig werden, aber man sollte nicht jetzt schon damit beginnen.
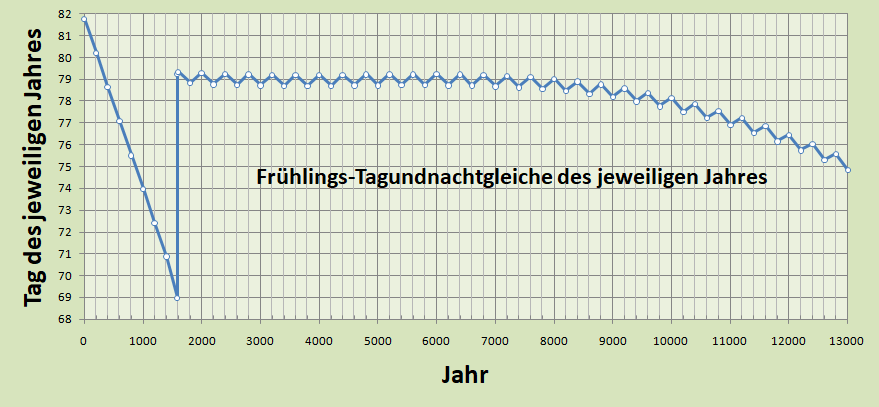
Die gegenwärtigen Abschätzungen laufen auf eine gute Stabilität bis etwa zum Jahr 7000 hinaus.
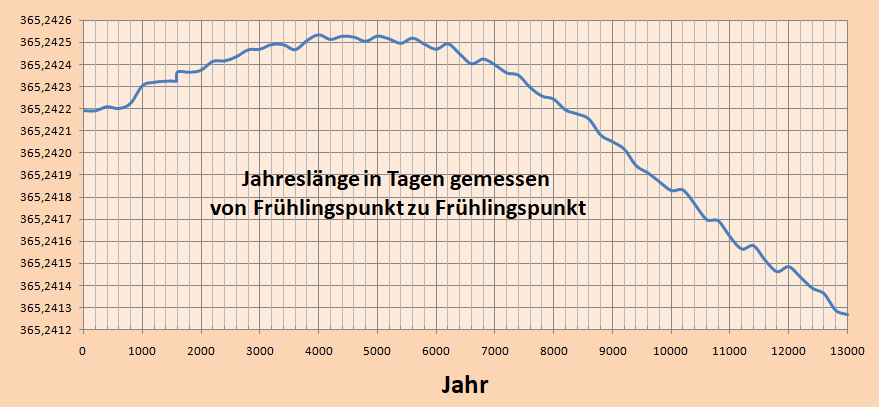
Bild 9
Das Zappeln der blauen Linie ist ein Ergebnis der Kalenderreform. Dabei bleibt alle 400 Jahre der Schalttag erhalten, der ansonsten an den vollen Jahrhunderten ausfällt.
Die Punkte auf der Linie sind aber alle 200 Jahre so dass jeder zweite Punkt um einen Tag hochspringt.
Bild 10
Die Erdrotation wird auf die Dauer langsamer und damit die Tage länger. Dadurch passen weniger dieser Tage in das Jahr, welches selbst sehr zeitstabil ist.
Ursache ist eine Drehmomentübertragung durch Gezeitenkräfte auf den Mond, der sich dadurch auch mehr von der Erde entfernt.
Diese gleichmäßige Abbremsung aufaddiert gibt eine quadratische Funktion (Parabel) für die Zeitdifferenz zwischen unserer alltäglichen Zeit,
die mit der Erdrotation durch Schaltsekunden synchronisiert ist,
und der gleichmäßig ablaufenden Atomzeit.
Sie wird, einschließlich kurzzeitigen Abweichungen mit ΔT (delta T) bezeichnet und bei den Sonnenfinsternissen angegeben.
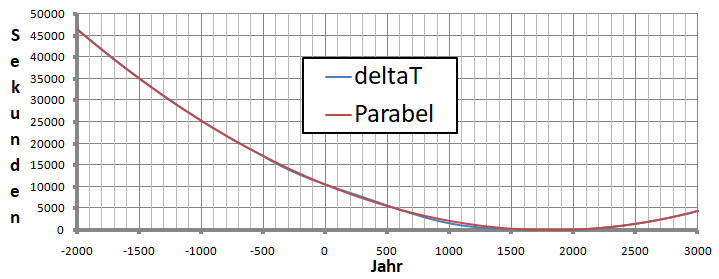
Bei einer Langzeitbetrachtung in Bild 11 über 5000 Jahre kann man kaum Unterschiede zwischen Parabel und ΔT sehen:
Bild 11
Kurzfristig gibt es aber Veränderungen durch Massenumlagerungen in und auf der Erde: Erdbeben, Schneeschmelze und vieles mehr.
Rückblickend sind historische Bericht von beobachteten Sonnenfinsternissen eine Möglichkeit, den tatsächlichen genauen Verlauf von ΔT zu bestimmen.
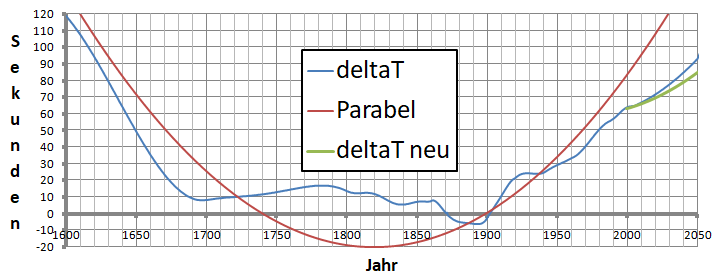
Seit der Erfindung von Teleskop und Pendeluhr sind auch schon Abweichung von der Parabelform in früherer Zeit dokumentiert, wie ein vergrößerter Ausschnitt von 450 Jahren aus obigem Bild in Bild 12 zeigt:
Bild 12
Dadurch ändern sich die bei den Finsternissen angegebenen Werte für ΔT.
In den letzten 10 Jahren hat sich die Erdrotation nicht so stark verringert wie vorausberechnet.
Es gab auch seit 2016 keine Einfügung von Schaltsekunden.
Die schon vor vielen Jahren vorausberechneten Sonnenfinsternisse von
Xavier M. Jubier
sind dadurch schon jetzt um 3 Sekunden früher, das heißt auch, dass der Finsternispfad sich um diese Zeit nach Westen verschiebt.
Die Abweichung von der Berechnung steigt voraussichtlich bis zum Ende des Jahrzehnts noch weiter an.
Eine so langfristige Betrachtung war wohl bei der Frage, ob es mehr totale Sonnenfinsternisse im Sommer gibt, nicht beabsichtigt.
Aber wie mit der Veränderung der Jahreszeitlängen auch das Klima auf der Nordhalbkugel beeinflusst wird, ist schon interessant.
5.) die Neumondtermine der nächsten Zeit
Nun aber zu überschaubaren Zeiträumen.
Es folgt Tabelle 2 mit einer Liste aller Neumond-Zeitpunkte für das Jahr 2024 und 2025.
Ein gutes Anwendungsbeispiel des Julianischen Datums in der Tabelle sind die Berechnungen der Zeiträume zwischen zwei Neumonden, auch Lunationsdauer genannt.
Dazu kommt noch die Lunationsnummer (LN oder L2000), eine Durchzählung der Neumonde ab einem festgelegten Zeitpunkt.
Hier wird die heute gebräuchlichste Zählung von
Jean Meeus verwendet, mit der Startnummer 0 am 6. Januar 2000.
Das ist aber nicht die einzige Zählung:
- Brown Lunation Number (BLN = LN + 953) Startnummer 1 am 17. Jan. 1923
- Goldstine Lunation Number (GLN = LN + 37105) Startnummer 0 am 1. Jan. -1000
- Thai Lunation Number (TLN = LN + 16843) Startnummer 0 am 24. März 638
- Islamic Lunation Number (ILN = LN + 17038) Startnummer 1 am 14. Juli 622
- Hebrew Lunation Number (HLN = LN + 71234) Startnummer 1 am 7. Sep. -3760
Die Daten sind alle gemäß Gregorianischem Kalender und einschließlich der Jahreszahl Null.
In der Bibel wird das Alter von Methusalem, dem Großvater von Noah, mit 969 Jahre angegeben, wahrscheinlich sind aber Lunationen gemeint, das sind dann 78 Jahre und 4 Monate.
| # |
Kalender Datum (UTC) |
Julianisches
Datum |
seit letztem
Neumond |
Magnitude |
Gamma |
Saros |
L2000 |
Typ |
| 1 | Do 11. Jan. 2024⠀12:00 | 2460321,0001 | 29,5197 | 1,00463 | -5,0122 | 248 | 297 | |
| 2 | Fr 9. Feb. 2024⠀23:04 | 2460350,4612 | 29,4611 | 1,02582 | -4,1823 | 286 | 298 | |
| 3 | So 10. Mrz. 2024⠀09:03 | 2460379,8774 | 29,4162 | 1,03830 | -2,2138 | 324 | 299 | |
| 4 | Mo 8. Apr. 2024⠀18:19 | 2460409,2638 | 29,3865 | 1,05674 | 0,3450 | 139 | 300 | T |
| 5 | Mi 8. Mai 2024⠀03:19 | 2460438,6385 | 29,3747 | 1,02812 | 2,8372 | 177 | 301 | |
| 6 | Do 6. Jun. 2024⠀12:36 | 2460468,0257 | 29,3871 | 1,00742 | 4,6444 | 215 | 302 | |
| 7 | Fr 5. Jul. 2024⠀22:58 | 2460497,4571 | 29,4314 | 0,98122 | 5,3001 | 253 | 303 | |
| 8 | So 4. Aug. 2024⠀11:13 | 2460526,9675 | 29,5104 | 0,95454 | 4,5656 | 291 | 304 | |
| 9 | Di 3. Sep. 2024⠀01:55 | 2460556,5800 | 29,6125 | 0,93238 | 2,5163 | 329 | 305 | |
| 10 | Mi 2. Okt. 2024⠀18:50 | 2460586,2854 | 29,7053 | 0,93269 | -0,3536 | 144 | 306 | R |
| 11 | Fr 1. Nov. 2024⠀12:49 | 2460616,0344 | 29,7490 | 0,91744 | -3,1630 | 182 | 307 | |
| 12 | So 1. Dez. 2024⠀06:21 | 2460645,7652 | 29,7308 | 0,92889 | -4,9760 | 220 | 308 | |
| 13 | Mo 30. Dez. 2024⠀22:27 | 2460675,4360 | 29,6708 | 0,95207 | -5,2341 | 258 | 309 | |
| 14 | Mi 29. Jan. 2025⠀12:40 | 2460705,0278 | 29,5918 | 0,98267 | -3,9484 | 296 | 310 | |
| 15 | Fr 28. Feb. 2025⠀00:48 | 2460734,5337 | 29,5059 | 1,01404 | -1,6106 | 111 | 311 | |
| 16 | Sa 29. Mrz. 2025⠀10:57 | 2460763,9564 | 29,4227 | 1,03908 | 1,0492 | 149 | 312 | P |
| 17 | So 27. Apr. 2025⠀19:27 | 2460793,3109 | 29,3545 | 1,05225 | 3,3277 | 187 | 313 | |
| 18 | Di 27. Mai 2025⠀03:00 | 2460822,6253 | 29,3144 | 1,05083 | 4,7145 | 225 | 314 | |
| 19 | Mi 25. Jun. 2025⠀10:33 | 2460851,9396 | 29,3143 | 1,03516 | 4,9244 | 263 | 315 | |
| 20 | Do 24. Jul. 2025⠀19:13 | 2460881,3011 | 29,3615 | 1,00833 | 3,8773 | 301 | 316 | |
| 21 | Sa 23. Aug. 2025⠀06:07 | 2460910,7550 | 29,4539 | 0,97566 | 1,7231 | 116 | 317 | |
| 22 | So 21. Sep. 2025⠀19:54 | 2460940,3294 | 29,5743 | 0,94384 | -1,0744 | 154 | 318 | P |
| 23 | Di 21. Okt. 2025⠀12:26 | 2460970,0187 | 29,6894 | 0,91946 | -3,7229 | 192 | 319 | |
| 24 | Do 20. Nov. 2025⠀06:49 | 2460999,7844 | 29,7656 | 0,90750 | -5,3318 | 230 | 320 | |
| 25 | Sa 20. Dez. 2025⠀01:44 | 2461029,5726 | 29,7882 | 0,91066 | -5,3118 | 268 | 321 | |
Tabelle 2
Man beachte die Zeilen, bei denen der Typ einer Sonnenfinsternis angegeben ist:
- T = total am 8. April 2024 (Mexiko)
- R = ringförmig am 2. Oktober 2024 (Osterinsel)
- P = partiell am 29. März 2025 (Kanada, Grönland, Norwegen)
- P = partiell am 21. September 2025 (Neuseeland)
Nur bei einem Gammawert im Bereich von -1 bis +1 sind totale oder ringförmige Finsternisse zu beobachten.
Die Magnitude macht den Unterschied zwischen total und ringförmig.
Bei partiellen Finsternissen liegt der Betrag von Gamma zwischen 1 und 1,5.
Positive Werte sind nahe des Nordpols und negative Werte nahe des Südpols zu beobachten.
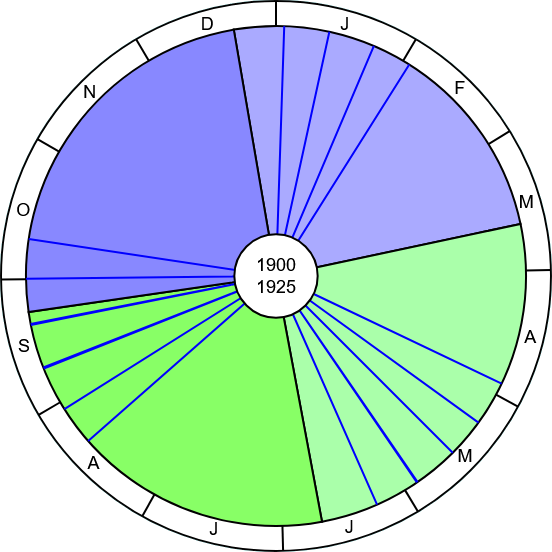
6.) totale Sonnenfinsternisse in Intervallen von 25 Jahren
Bild 13
| 1900 |
1925 |
1950 |
1975 |
2000 |
2025 |
2050 |
2075 |
2100 |
| Sommer | 12 |
11 |
10 |
6 |
8 |
12 |
13 |
13 |
$\Sigma$=85 |
| Winter | 6 |
9 |
9 |
11 |
7 |
5 |
4 |
7 |
$\Sigma$=58 |
|
Start und Stopp des automatischen Durchlaufs durch diese Tabelle und in Bild 13
|
Tabelle 3
Der "Windrad-Effekt" beim automatischen Durchlauf aller totalen Sonnenfinsternisse über zwei Jahrhunderte ist keine Eigenschaft nur der Gegenwart.
Auch in alle anderen Jahrtausenden sieht das genau so aus, auch wenn die genauen Zahlen etwas variieren.
Es gibt vor allem aber auch Intervalle, die in der Sommerzeit besonders benachteiligt oder bevorzugt werden.
Das ist kein Wunder, wenn man sich die Entstehung ansieht:
manchmal liegen zwei "Flügel" im Sommerhalbjahr und manchmal im Winterhalbjahr.
Das Verhältnis der Summen über 200 Jahre (rechts außen in Tabelle 3:
$\frac{85}{58}≈1,4655)$ zeigt aber schon eine deutliche Tendenz zu mehr Sommerereignissen.
Was aber ist die Ursache für den "Windrad-Effekt"? Es sind die Zyklen aus Tabelle 4.
Die jeweiligen Zyklen beinhalten keine "eignen" Finsternisse, sondern alle Finsternisse sind Elemente in allen Zyklen.
Diese Vernetzung sorgt für den Effekt. Die kurzfristigen Zyklen sind für das Aussehen verantwortlich und die langfristigen für die Drehung.
Übrigens zeigen die ringförmigen Sonnenfinsternisse den gleichen Effekt. Sie liegen mit ihren "Flügeln" in den freien Flächen genau zwischen den totalen Finsternissen.
Zyklus
Name | synodische
Monate | Jahre | Anzahl der
Finsternisse | Lebensdauer
in Jahre |
|---|
| Semester | 6 | 0,485 | 9,25 | 4,0 |
| Hepton | 41 | 3,31 | 14,2 | 43,7 |
| Octon | 47 | 3,80 | 22,9 | 83,2 |
| Anonymos | 88 | 7,11 | 35 | 241,7 |
| Tritos | 135 | 10,92 | 65,1 | 700 |
| Saros | 223 | 18,03 | 70,6 | 1255 |
| Inex | 358 | 28,95 | 809 | 23390 |
Tabelle 4
Eine weitaus vollständigere Liste und deren Eigenschaften findet sich
hier.
7.) Saros-Inex-Panorama
Bild 14
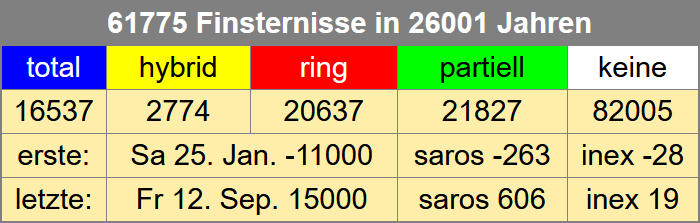
Das Bild 14 zeigt das Saros-Inex-Panorama auf einer Fläche von 910 ⋅ 158 = 143780 Pixel.
Davon sind 61775 farbige Pixel als Stellvertreter einer Sonnenfinsternis und 82005 weiße Pixel als Neumondtermine ohne Finsternis.
Die Bedeutung der Farben ist in Tabelle 5 gelistet.
Ein Zeitraum von heute ± 13000 Jahre ist damit abgedeckt.
Das Bild stammt aus WIKIPEDIA,
musste aber nachbearbeitet werden, weil 873 Abweichungen zur EXCEL-Version der
NASA sich zeigten.
Das hört sich sehr viel an aber bis auf eine totale Sonnenfinsternis am rechten Rand des Bildes
waren nur partielle Finsternisse entlang des unteren Randes die Ursache der Unterschiede.
Wer den Fehler verursacht hat ist unbekannt.
Jetzt ist absolute Übereinstimmung der Bildpixel mit der EXCEL-Version.
Alle Kalenderdaten sind ausschließlich nach dem Gregorianischen Kalender angegeben.
Ansonsten würden sich vor ein paar Tausend Jahren Daten in falschen Jahreszeiten ergeben,
das war ja das Problem mit dem Julianischen Kalender und Anlass zur Kalenderreform im Jahre 1582.
Tabelle 5
Das Diagramm wurde erstmalig erzeugt von dem niederländischen Amateurastronomen George van den Bergh (* 25. April 1890, † 3. Oktober 1966).
Er hatte das Schema aber nur mit den ca. 8000 Finsternissen aus dem "Canon der Finsternisse (1885)"
von Theodor Oppolzer (* 26. Oktober 1841 in Prag; † 26. Dezember 1886 in Wien) gefüllt.
Die Anordnung ist so gewählt, dass in horizontalen Zeilen von oben nach unten jeweils die von van den Bergh gewählten Nummern des INEX-Zyklusses -59 bis 98
und in vertikalen Spalten von links nach rechts die Nummern des SAROS-Zyklusses fortlaufend von -289 bis 620 platziert sind.
Auch wenn die von George van den Bergh festgelegte Zählung willkürlich ist, so wird immer noch zumindest die Saros-Nr. zu jeder Sonnenfinsternis nach diesem Schema angegeben.
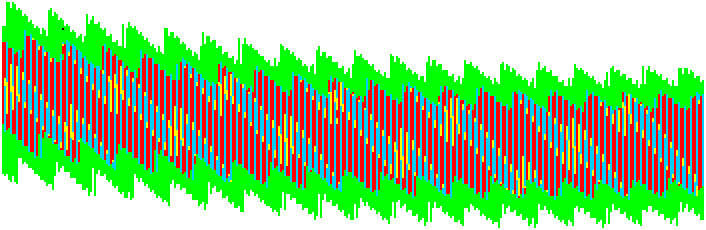
Das folgende Bild 15 ist ein vergrößerter Ausschnitt aus der Mitte von Bild 14.
Es umfasst einen Zeitbereich von heute ± 6000 Jahre. Das ist von Saros-Nr. -30 bis 320.
Zur Orientierung ist der Ursprung des Koordinatensystems Saros-Nr. = Inex-Nr. = 0 als schwarzes Pixel links oben im grünen Bereich markiert.
Bild 15
| Position | Saros | Inex | Datum (gregorianisch) | Jul. Datum | Lunation |
|---|
| schwarzes Pixel | 0 | 0 | Di 12. Jun. -2883⠀04:52 | 668227,7033 | -60389 |
| rechtes Nachbar-Pixel | 1 | 0 | Do 23. Mai -2854⠀04:46 | 678799,6986 | -60389+358 |
| unteres Nachbar-Pixel | 0 | 1 | So 23. Jun. -2865⠀12:35 | 674813,0243 | -60389+223 |
Bei den Darstellungen der Panoramen ist der Zusammenhang zwischen den Finsternistypen nicht erkennbar
und der zeitliche Verlauf kann auch nur grob von links oben nach rechts unten erahnt werden.
Deshalb ist eine andere Anordnung der gleichen Pixel aufschlussreicher.
Dazu finden zunächst folgende Berechnungen statt:
- aus dem Pixel mit bekannter Saros- und Inex-Nr. und bekannter Farbe wird das Datum des zugehörigen Neumonds ermittelt
- zu diesem Datum werden Abstand der Sonne und des Mondes sowie die ekliptikale Breite der Mondes berechnet
- daraus lässt sich der Wert von Gamma und die Magnitude bestimmen
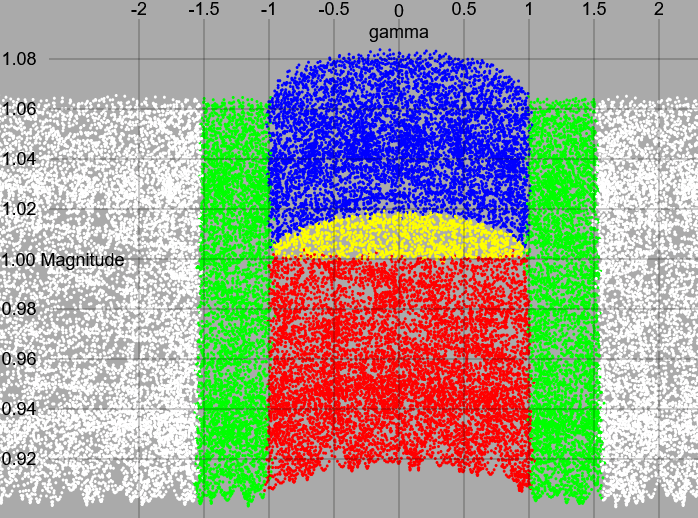
Nun wird jedes Pixel aus Bild 15 in ein neues Diagramm mit den Koordinaten Gamma und Magnitude eingetragen:
Bild 16
In diesem Diagramm finden sich die verschiedenen Farben der Finsternistypen zu großen Flächen zusammen.
Sehr deutlich wird die horizontale Grenze zwischen rot (ringförmig) und gelb+blau (total) bei einer Magnitude von 1,00 erkennbar.
Die vertikalen Grenzen durch Betrag von Gamma zwischen 1,0 und 1,5 zäunen die grünen (partiellen) Bereiche ein.
Die weißen Bereiche außen sind auch Neumonde mit Saros- und Inex-Nr. aber die Finsternisse können nur von GPS-Satelliten in hohen Orbits über den Polen gesehen werden.
Aber auch in diesem Diagramm ist eine zeitliche Anordnung noch nicht zu erkennen.
Das ändert sich, wenn nicht gleichzeitig alle Saroszyklen übereinander gezeichnet werden.
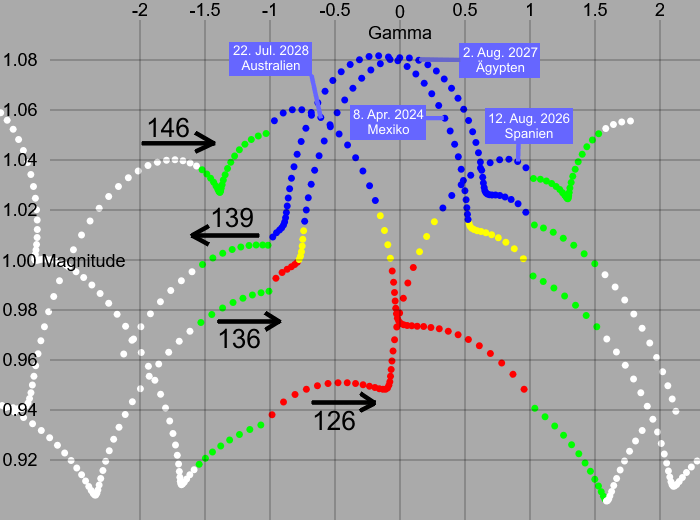
Im folgenden Bild 17 ist nur eine Auswahl von 4 Saroszyklen der Gegenwart dargestellt.
Bild 17
Die "Perlenkette" jedes Saroszyklusses liegt in streng zeitlicher Reihenfolge vor.
Die Richtung (siehe Pfeile) ist bei geradzahligen Nummern nach rechts, das ist auf der Erde nach Norden, die ungeradzahligen Nummern gehen nach links, also nach Süden.
Die Zeit zwischen zwei "Perlen" ist genau 223 Neumonde,
das sind durchschnittlich 6585,32 Tage oder 18,03 Jahre.
Die "Perlen" sind durchnummeriert, das sind die Inex-Nummern.
Hier gibt es ein "lebendiges" Diagramm, bei dem die Saros-Nummern frei gewählt werden können und
wenn die Maus auf eine "Perle" zeigt wird ein Fenster sich öffnen und die Daten zu der Finsternis erscheinen.
8.) Statistik mit größeren Zahlen
Wie sich bisher aus den obigen Ausführungen abzeichnet, sind bei kleinen Zahlen von totalen Sonnenfinsternissen keine zuverlässigen Aussagen über deren Häufigkeit im Sommer zu machen.
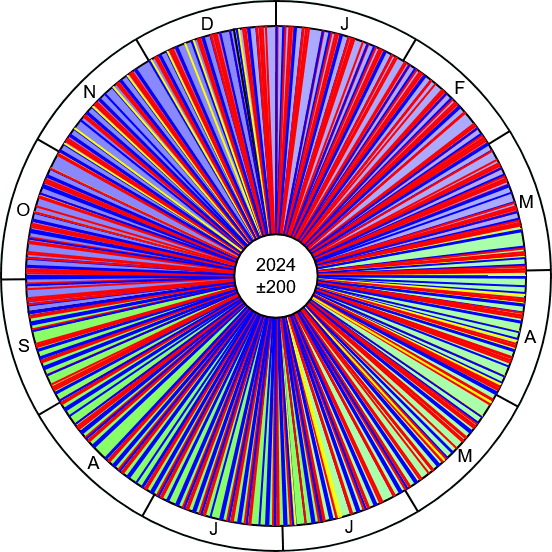
Deshalb ist im folgenden Bild 18 in Verbindung mit der Tabelle 6 eine größere Zeitspanne für die Statistik auswählbar.
Bild 18
| 2024 |
±25 |
±50 |
±100 |
±200 |
±400 |
±800 |
2024 |
| Sommer |
21 |
39 |
79 |
158 |
306 |
586 |
Sommer |
| Winter |
12 |
27 |
59 |
110 |
216 |
433 |
Winter |
| $\frac{\rm Sommer}{\rm Winter}$ |
1,75 |
1,44 |
1,34 |
1,44 |
1,42 |
1,35 |
$\frac{\rm Sommer}{\rm Winter}$ |
Start und Stopp eines automatischen Durchlaufs
durch diese Tabelle und Anzeige in Bild 18
|
Tabelle 6
Ab einer Zeitspanne von 400 Jahren zeigt das Bild 18 eine ausreichend gleichmäßige Füllung.
Eine weitere Vergrößerung bringt keine wesendliche Änderung oder Schwankung.
Das Verhältnis von Sommerhalbjahr zu Winterhalbjahr pendelt sich bei etwa 1,4 ein.
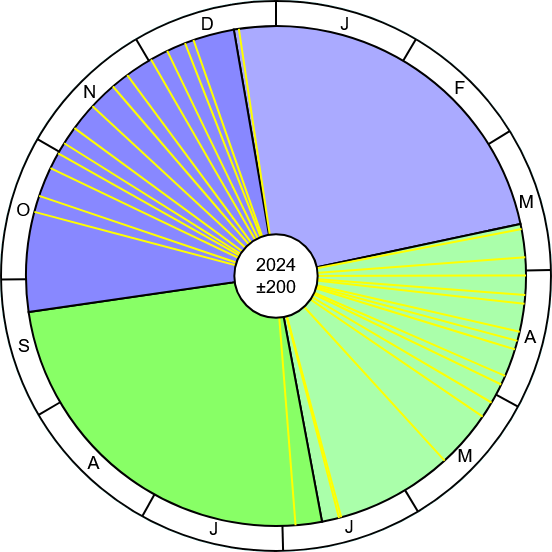
Um festzustellen, ob die Gleichmäßigkeit keine Täuschung ist, kann man sich mal ansehen, welches Bild entsteht,
wenn man nicht nur totale sondern auch ringförmige und hybride Finsternisse für den gleichen Zeitraum durchzählt und anzeigt:
Bild 19
| Typ | Sommer | Winter | Verhältnis |
|---|
| ring | 137 | 176 | 0,778 |
| total | 158 | 110 | 1,436 |
| hybrid | 16 | 14 | 1,143 |
| Summe | 311 | 300 | 1,037 |
Tabelle 7
Hier erkennt man, dass nur noch die unterschiedlichen Längen der Jahreszeiten (siehe oben) zu einem leichten Überschuss im Sommerhalbjahr kommen.
Der Einfluss der hybriden Sonnenfinsternisse ist durch ihre Zahl gering, aber ihre Verteilung sehr eigenartig.
Alle sind über einige Jahrhunderte nur im Frühling und Herbst:
Bild 20
Wer gerne eigene Statistiken mit den zugehörigen Bildern und Listen anfertigen will hat hier alle Möglichkeiten.
Zusammengefasst: kurzfristige Zeiträume zeigen keine eindeutige Bevorzugung von totalen Sonnenfinsternissen im Sommer (siehe "Windradeffekt" Abs. 6),
aber langfristig gibt es eine klare Mehrheit.
Obwohl die Sonnenferne und die Verlängerung der zugehörigen Jahreszeiten immer eine feste Kopplung aufweisen, kann man statistisch beide Einflüsse voneinander trennen:
Sonnenferne wirkt sich 10 mal stärker aus als die Verlängerungen der sommerlichen Jahreszeiten.
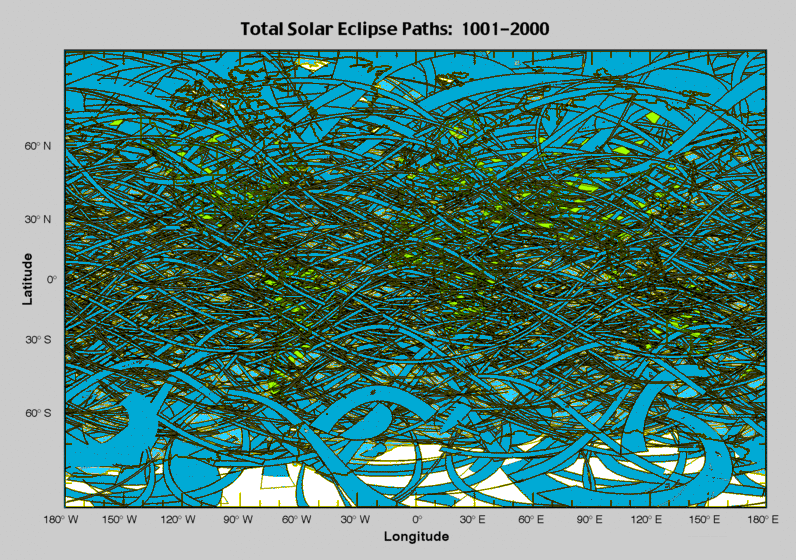
Einen grafischen Beweis liefert zudem das folgende Bild 21 aus Wikipedia.
Es ist deutlich zu erkennen, dass die südliche Polarregion weniger totale Sonnenfinsternisse zeigt als die nördliche Polarregion.
Es ist eine Folge der unterschiedlichen Beleuchtungsverhältnisse. Der Südpol und seine Umgebung liegt im Sommer in dauernder Dunkelheit.
Andererseits liegt der Nordpol im Winter im Dunkeln aber dann werden auch nicht so viele totale Sonnenfinsternisse verpasst.
Bild 21
9.) Formel-Anhang (PHP)
Die folgenden Formeln stammen aus dem Buch:
Oliver Montenbruck "Grundlagen der Ephemeridenrechnung"
Verlag Sterne und Weltraum Taschenbuch 10 München 1985
ISBN 3-87973-913-7
Es wurden nur Anpassungen an die Programmiersprache PHP vorgenommen.
$Arc = pi() / 180;
//==============================================
//Winkelfunktionen mit Argumenten in Grad
//==============================================
function gsin($phi){
global $Arc;
return sin($phi * $Arc);
}
function gcos($phi){
global $Arc;
return cos($phi * $Arc);
}
//==============================================
// Signum-, Fix-, Integer- und Cint-Funktion
//==============================================
function sgn($val){
return $val == 0 ? 0 : ($val > 0 ? 1 : -1);
}
function fix($number){
return sgn($number) * floor(abs($number));
}
function int($number){
return floor($number);
}
function Cint($number){
return round($number,0);
}
zurück zur Übersicht
//==============================================
//erzeugt ekliptikale Länge der Sonne in Grad
//==============================================
function Sonne_Laenge($JDatum){
$T = ($JDatum - 2415020) / 36525;
$DLP = ((1.882 - 0.016 * $T) * gsin(57.24 + 150.27 * $T)
+ 6.4 * gsin(231.19 + 20.2 * $T)
+ 0.266 * gsin(31.8 + 119 * $T)) / 3600;
$L0 = 279.6966778 + 36000.768925 * $T + 0.0003025 * $T * $T
+ 0.202 / 3600 * gsin(315.6 + 893.3 * $T) + $DLP;
$g = 358.4758333 + 35999.04975 * $T - 0.00015 * $T * $T + $DLP; //mittl. Anomalie Sonne
$G2 = 212.45 + 58517.493 * $T; //mittl. Anomalie Venus
$G4 = 319.58 + 19139.977 * $T; //mittl. Anomalie Mars
$G5 = 225.28 + 3034.583 * $T + 1300 / 3600 * gsin(133.775 + 39.804 * $T); //mittl. Anomalie Jupiter
$D = 350.737486 + 445267.114217 * $T; //mittl. Winkel Sonne-Mond
$DL = (1.919460278 - 0.004788888 * $T) * gsin($g)
+ (0.020093889 - 0.000100278 * $T) * gsin(2 * $g)
+ 0.000292778 * $T * gsin(3 * $g); //Sonne
$DL2 = 4.838 * gcos(299.102 + $G2 - $g) +
5.526 * gcos(148.313 + 2 * $G2 - 2 * $g) +
2.497 * gcos(315.943 + 2 * $G2 - 3 * $g) +
1.559 * gcos(345.253 + 3 * $G2 - 4 * $g) +
1.024 * gcos(318.15 + 3 * $G2 - 5 * $g); //Venus
$DL4 = 2.043 * gcos(343.888 - 2 * $G4 + 2 * $g) +
1.77 * gcos(200.402 - 2 * $G4 + $g); //Mars
$DL5 = 7.208 * gcos(179.532 - $G5 + $g) +
2.6 * gcos(263.217 - $G5) +
2.731 * gcos(87.145 - 2 * $G5 + 2 * $g); //Jupiter
$DLM = 6.454 * gsin($D); //Mond
$lamda = ($L0 + $DL + ($DL2 + $DL4 + $DL5 + $DLM) / 3600) / 360;
$el = $lamda - int($lamda);
If($el > 0.5) {$el = $el - 1;}
return $el * 360;
}
zurück zur Übersicht
//==============================================
//erzeugt ekliptikale Länge des Mondes in Grad
//==============================================
function Mond_Laenge($JDatum){
$T = ($JDatum - 2415020) / 36525;
$T2 = $T * $T;
$kl = 270.434164 + 481267.883142 * $T - 0.001133 * $T2;
$M = 296.104608 + 477198.849108 * $T + 0.009192 * $T2;
$O = 259.183275 - 1934.142008 * $T + 0.002078 * $T2;
$l = 279.696678 + 36000.768925 * $T + 0.000303 * $T2;
$n = 358.475833 + 35999.04975 * $T - 0.00015 * $T2;
$L1 = 22640 * gsin($M) + 769 * gsin(2 * $M) + 36 * gsin(3 * $M);
$L2 = -125 * gsin($kl - $l) + 2370 * gsin(2 * ($kl - $l));
$l3 = -668 * gsin($n) - 412 * gsin(2 * ($kl - $O));
$l4 = 212 * gsin(2 * ($kl - $l - $M)) + 4586 * gsin(2 * ($kl - $l) - $M);
$l5 = 192 * gsin(2 * ($kl - $l) + $M) + 165 * gsin(2 * ($kl - $l) - $n);
$l6 = 206 * gsin(2 * ($kl - $l) - $M - $n) - 110 * gsin($M + $n) + 148 * gsin($M - $n);
$lamda = ($kl + ($L1 + $L2 + $l3 + $l4 + $l5 + $l6) / 3600) / 360;
$el = $lamda - int($lamda);
if($el > 0.5) {$el = $el - 1;}
return $el * 360;
}
zurück zur Übersicht
//==============================================
//erzeugt ekliptikale Breite des Mondes in Grad
//==============================================
function Mond_Breite($JDatum){
$T = ($JDatum - 2415020) / 36525;
$T2 = $T * $T;
$kl = 270.434164 + 481267.883142 * $T - 0.001133 * $T2;
$M = 296.104608 + 477198.849108 * $T + 0.009192 * $T2;
$O = 259.183275 - 1934.142008 * $T + 0.002078 * $T2;
$l = 279.696678 + 36000.768925 * $T + 0.000303 * $T2;
$n = 358.475833 + 35999.04975 * $T - 0.00015 * $T2;
$L1 = 22640 * gsin($M) + 769 * gsin(2 * $M) + 36 * gsin(3 * $M);
$L2 = -125 * gsin($kl - $l) + 2370 * gsin(2 * ($kl - $l));
$L3 = -668 * gsin($n) - 412 * gsin(2 * ($kl - $O));
$L4 = 212 * gsin(2 * ($kl - $l - $M)) + 4586 * gsin(2 * ($kl - $l) - $M);
$L5 = 192 * gsin(2 * ($kl - $l) + $M) + 165 * gsin(2 * ($kl - $l) - $n);
$L6 = 206 * gsin(2 * ($kl - $l) - $M - $n) - 110 * gsin($M + $n) + 148 * gsin($M - $n);
$lamda = $kl + ($L1 + $L2 + $L3 + $L4 + $L5 + $L6) / 3600;
$b1 = 18520 * gsin($lamda - $O + 412 / 3600 * gsin(2 * ($kl - $O)) + 541 / 3600 * gsin($n));
$b2 = -526 * gsin(2 * $l - $kl - $O);
$b3 = 44 * gsin(2 * $l - $kl - $O + $M);
$b4 = -31 * gsin(2 * $l - $kl - $O - $M);
$b5 = -23 * gsin(2 * $l - $kl - $O + $n);
$b6 = 11 * gsin(2 * $l - $kl - $O - $n);
$b7 = -25 * gsin($kl - $O - 2 * $M);
$b8 = 21 * gsin($kl - $O - $M);
$beta = ($b1 + $b2 + $b3 + $b4 + $b5 + $b6 + $b7 + $b8) / 3600 / 360;
return ($beta - Cint($beta)) * 360;
}
zurück zur Übersicht
//==============================================
// erzeugt Zeitpunkt der Mondphase als Julianisches Datum
// Phase = 0 ist Neumond, Phase = 90 ist letztes Viertel usw.
// move ist optional: 1 = nächster, 0 = vorheriger
//==============================================
function Mondphase_nach($JDatum, $Phase, $move = 1){
$JDatum = $JDatum + 0.000005;
$M = 29.530589;
$p = (Sonne_Laenge($JDatum) - Mond_Laenge($JDatum) - $Phase) / 360;
if($move==1) {$p = $p-int($p);} else {$p = $p-fix($p)+$move;}
$z = $p * $M + $JDatum;
do{
$p = (Sonne_Laenge($z) - Mond_Laenge($z) - $Phase) / 360;
If($p < -0.5) {$p = $p + 1;}
If($p > 0.5) {$p = $p - 1;}
$z += ($p - fix($p)) * $M;
}
while (abs($p) > 0.000001);
return $z;
}
zurück zur Übersicht
//==============================================
// Sonnenabstand in Astronomische Einheiten
// für den Abstand in km mit 149597870.7 multiplizieren
//==============================================
function Sonnenabstand($JDatum){
$T = ($JDatum - 2415020) / 36525;
$DLP = (1.882 / 3600 - 0.016 / 3600 * $T) * gsin(57.24 + 150.27 * $T)
+ 6.4 / 3600 * gsin(231.19 + 20.2 * $T) + 0.266 / 3600 * gsin(31.8 + 119 * $T);
$g = 358.4758333 + 35999.04975 * $T - 0.00015 * $T * $T + $DLP;
$G2 = 212.45 + 58517.493 * $T;
$G4 = 319.58 + 19139.977 * $T;
$G5 = 225.28 + 3034.583 * $T + 1300 / 3600 * gsin(133.775 + 39.804 * $T);
$G6 = 175.6 + 1221.794 * $T;
$D = 350.737486 + 445267.114217 * $T;
$A = 296.104608 + 477198.849108 * $T;
$U = 11.250889 + 483202.02515 * $T;
$DL = (1.919460278 - 0.004788888 * $T) * gsin($g)
+ (0.020093889 - 0.000100278 * $T) * gsin(2 * $g)
+ 0.000292778 * $T * gsin(3 * $g);
$R0 = (0.00003057 - 0.00000015 * $T)
+ (-0.00727412 + 0.00001814 * $T) * gcos($g)
+ (-0.00009138 + 0.00000046 * $T) * gcos(2 * $g)
- 0.00000145 * gcos(3 * $g);
$DR2 = (2359 * gcos(209.08 + $G2 - $g) + 160 * gcos(58.4 + 2 * $G2 - $g)
+ 6842 * gcos(58.318 + 2 * $G2 - 2 * $g) + 869 * gcos(226.7 + 2 * $G2 - 3 * $g)
+ 1045 * gcos(87.57 + 3 * $G2 - 3 * $g) + 1497 * gcos(255.25 + 3 * $G2 - 4 * $g)
+ 194 * gcos(49.5 + 3 * $G2 - 5 * $g) + 376 * gcos(116.28 + 4 * $G2 - 4 * $g)
+ 196 * gcos(105.2 + 4 * $G2 - 5 * $g) + 163 * gcos(145.4 + 5 * $G2 - 5 * $g)
+ 141 * gcos(105.4 + 5 * $G2 - 7 * $g)) / pow(10, 9);
$DR4 = (150 * gcos(127.7 - $G4 + $g) + 2057 * gcos(253.828 - 2 * $G4 + 2 * $g)
+ 151 * gcos(295 - 2 * $G4 + $g) + 168 * gcos(203.5 - 3 * $G4 + 3 * $g)
+ 215 * gcos(249 - 3 * $G4 + 2 * $g) + 478 * gcos(15.17 - 4 * $G4 + 3 * $g)
+ 105 * gcos(65.9 - 4 * $G4 + 2 * $g) + 107 * gcos(324.6 - 5 * $G4 + 4 * $g)
+ 139 * gcos(137.3 - 6 * $G4 + 4 * $g)) / pow(10, 9);
$DR5 = (208 * gcos(112 - $G5 + 2 * $g) + 7067 * gcos(89.545 - $G5 + $g)
+ 244 * gcos(338.6 - $G5) + 103 * gcos(350.5 - 2 * $G5 + 3 * $g)
+ 4026 * gcos(357.108 - 2 * $G5 + 2 * $g) + 1459 * gcos(19.467 - 2 * $G5 + $g)
+ 281 * gcos(81.2 - 3 * $G5 + 3 * $g) + 803 * gcos(352.56 - 3 * $G5 + 2 * $g)
+ 174 * gcos(8.6 - 3 * $G5 + $g) + 113 * gcos(347.7 - 4 * $G5 + 2 * $g)) / pow(10, 9);
$DR6 = (429 * gcos(10.6 - $G6 + $g) + 162 * gcos(200.6 - 2 * $G6 + 2 * $g)
+ 112 * gcos(203.1 - 2 * $G6 + $g)) / pow(10, 9);
$DRM = (13360 * gcos($D) + 370 * gcos($D + $A) - 1330 * gcos($D - $A) - 140 * gcos($D + $g) + 360 * gcos($D - $g)) / pow(10, 9);
return pow(10, $R0 + $DR2 + $DR4 + $DR5 + $DR6 + $DRM);
}
zurück zur Übersicht
//==============================================
// Mondabstand in Kilometer
//==============================================
function Mondabstand($JDatum){
return 6378.14 / gsin(MondHP($JDatum));
}
//==============================================
// Mond-Horizontal-Paralaxe
//==============================================
function MondHP($JDatum){
$T = ($JDatum - 2415020) / 36525;
$M = 296.104608 + 477198.849108 * $T + 0.009192 * $T * $T;
$kl = 270.434164 + 481267.883142 * $T - 0.001133 * $T * $T;
$l = 279.696678 + 36000.768925 * $T + 0.000303 * $T * $T;
return 3423 / 3600 + 187 / 3600 * gcos($M) + 10 / 3600 * gcos(2 * $M)
+ 34 / 3600 * gcos(2 * ($kl - $l) - $M)
+ 28 / 3600 * gcos(2 * ($kl - $l))
+ 3 / 3600 * gcos(2 * ($kl - $l) + $M);
}
Diese Informationen wurden zusammengestellt von